Binary Tree - 二叉树

二叉树是每个节点最多有两个子树的树结构，子树有左右之分，二叉树常被用于实现二叉查找树和二叉堆。

二叉树的第i层至多有 $2^{i-1}$ 个结点；深度为k的二叉树至多有 $2^k-1$ 个结点；对任何一棵二叉树T，如果其终端结点数为 $n_0$, 度为2的结点数为 $n_2$, 则 $n_0=n_2+1$。

一棵深度为 $k$, 且有 $2^k-1$ 个节点称之为满二叉树；深度为 $k$，有 $n$ 个节点的二叉树，当且仅当其每一个节点都与深度为 $k$ 的满二叉树中，序号为 $1$ 至 $n$ 的节点对应时，称之为完全二叉树。完全二叉树中重在节点标号对应。

树的遍历

从二叉树的根节点出发，节点的遍历分为三个主要步骤：对当前节点进行操作（称为“访问”节点，或者根节点）、遍历左边子节点、遍历右边子节点。访问节点顺序的不同也就形成了不同的遍历方式。需要注意的是树的遍历通常使用递归的方法进行理解和实现，在访问元素时也需要使用递归的思想去理解。

按照访问根元素(当前元素)的前后顺序，遍历方式可划分为如下几种：

• 深度优先：先访问子节点，再访问父节点，最后访问第二个子节点。根据根节点相对于左右子节点的访问先后顺序又可细分为以下三种方式。
  1. 前序(pre-order)：先根后左再右
  2. 中序(in-order)：先左后根再右
  3. 后序(post-order)：先左后右再根
• 广度优先：先访问根节点，沿着树的宽度遍历子节点，直到所有节点均被访问为止。

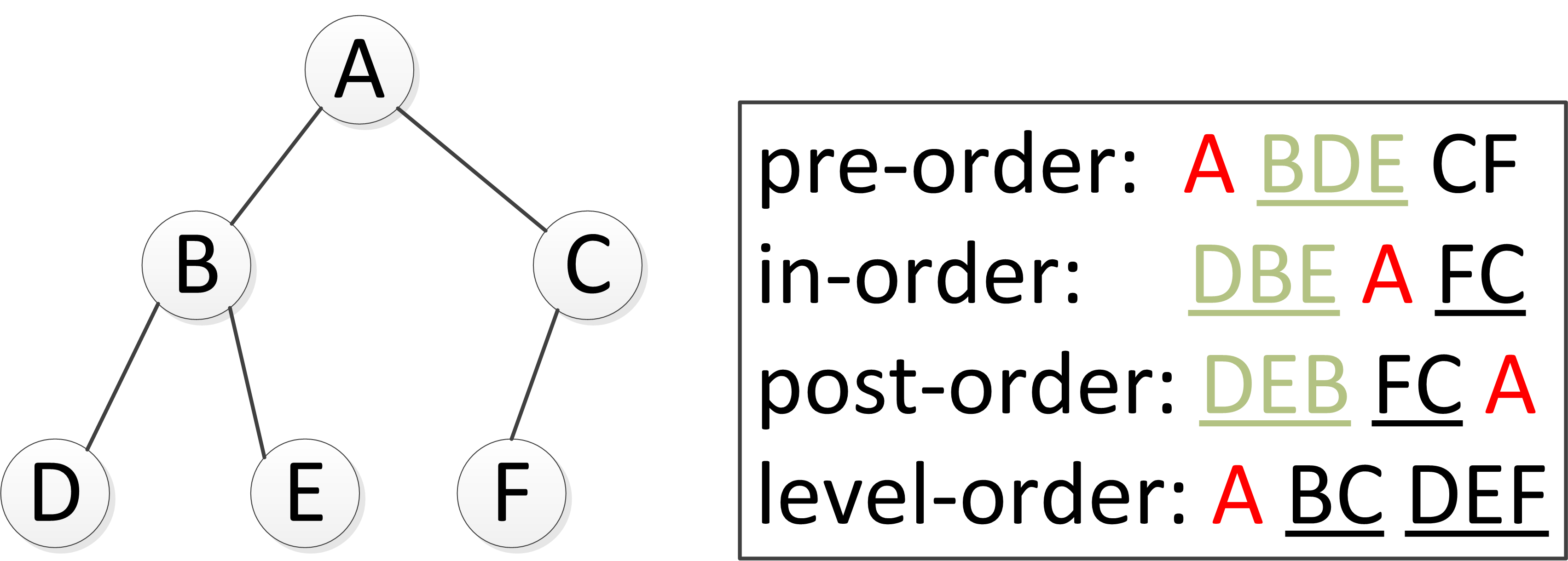
如下图所示，遍历顺序在右侧框中，红色A为根节点。使用递归和整体的思想去分析遍历顺序较为清晰。

二叉树的广度优先遍历和树的前序/中序/后序遍历不太一样，前/中/后序遍历使用递归，也就是栈的思想对二叉树进行遍历，广度优先一般使用队列的思想对二叉树进行遍历。

节点定义

这里的节点统一使用LeetCode的定义

struct TreeNode {
      int val;
      TreeNode *left;
      TreeNode *right;
      TreeNode(int x) : val(x), left(NULL), right(NULL) {}
  };

相关算法——递归法遍历

pre-order travese

相关算法——分治法（Divide & Conquer)

在计算机科学中，分治法是一种很重要的算法。分治法即“分而治之”，把一个复杂的问题分成两个或更多的相同或相似的子问题，再把子问题分成更小的子问题……直到最后子问题可以简单的直接求解，原问题的解即子问题的解的合并。这个思想是很多高效算法的基础，如排序算法（快速排序，归并排序）等。

分治法思想

• 分治法所能解决的问题一般具有以下几个特征：

  1. 问题的规模缩小到一定的程度就可以容易地解决。
  2. 问题可以分解为若干个规模较小的相同问题，即该问题具有最优子结构性质。
  3. 利用该问题分解出的子问题的解可以合并为该问题的解。
  4. 该问题所分解出的各个子问题是相互独立的，即子问题之间不包含公共的子问题。

• 分治法的三个步骤是：

  1. 分解（Divide）：将原问题分解为若干子问题，这些子问题都是原问题规模较小的实例。
  2. 解决（Conquer）：递归地求解各子问题。如果子问题规模足够小，则直接求解。
  3. 合并（Combine）：将所有子问题的解合并为原问题的解。

• 分治法的经典题目：

  1. 二分搜索
  2. 大整数乘法
  3. Strassen矩阵乘法
  4. 棋盘覆盖
  5. 归并排序
  6. 快速排序
  7. 循环赛日程表
  8. 汉诺塔

树类题的复杂度分析

对树相关的题进行复杂度分析时可统计对每个节点被访问的次数，进而求得总的时间复杂度。