- algorithm-reading
- leetcode/lintcode题解/算法学习笔记
- 1. Part I - Basics
- 2. Data Structure
- 3. Basics Sorting
- 4. Basics Misc
- 5. Part II - Coding
- 6. String - 字符串
-
7.
Integer Array - 整型数组
- 7.1. Remove Element
- 7.2. Zero Sum Subarray
- 7.3. Subarray Sum K
- 7.4. Subarray Sum Closest
- 7.5. Product of Array Exclude Itself
- 7.6. Partition Array
- 7.7. First Missing Positive
- 7.8. 2 Sum
- 7.9. 3 Sum
- 7.10. 3 Sum Closest
- 7.11. Remove Duplicates from Sorted Array
- 7.12. Remove Duplicates from Sorted Array II
- 7.13. Merge Sorted Array
- 7.14. Merge Sorted Array II
- 7.15. Median
-
8.
Binary Search - 二分搜索
- 8.1. Binary Search
- 8.2. Search Insert Position
- 8.3. Search for a Range
- 8.4. First Bad Version
- 8.5. Search a 2D Matrix
- 8.6. Find Peak Element
- 8.7. Search in Rotated Sorted Array
- 8.8. Find Minimum in Rotated Sorted Array
- 8.9. Search a 2D Matrix II
- 8.10. Median of two Sorted Arrays
- 8.11. Sqrt x
- 8.12. Wood Cut
- 9. Math and Bit Manipulation - 数学技巧与位运算
-
10.
Linked List - 链表
- 10.1. Remove Duplicates from Sorted List
- 10.2. Remove Duplicates from Sorted List II
- 10.3. Remove Duplicates from Unsorted List
- 10.4. Partition List
- 10.5. Two Lists Sum
- 10.6. Two Lists Sum Advanced
- 10.7. Remove Nth Node From End of List
- 10.8. Linked List Cycle
- 10.9. Linked List Cycle II
- 10.10. Reverse Linked List
- 10.11. Reverse Linked List II
- 10.12. Merge Two Sorted Lists
- 10.13. Merge k Sorted Lists
- 10.14. Reorder List
- 10.15. Copy List with Random Pointer
- 10.16. Sort List
- 10.17. Insertion Sort List
- 10.18. Check if a singly linked list is palindrome
- 11. Reverse - 翻转法
- 12. Binary Tree - 二叉树
- 13. Binary Search Tree - 二叉搜索树
- 14. Exhaustive Search - 穷竭搜索
- 15. Dynamic Programming - 动态规划
- 16. Appendix I Interview and Resume
Merge Sort - 归并排序
核心:将两个有序对数组归并成一个更大的有序数组。通常做法为递归排序,并将两个不同的有序数组归并到第三个数组中。
先来看看动图,归并排序是一种典型的分治应用。
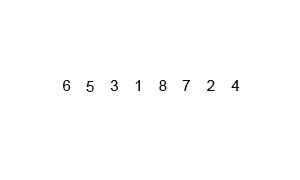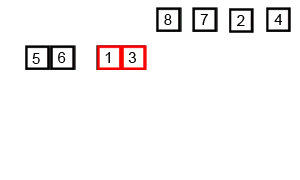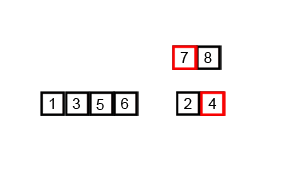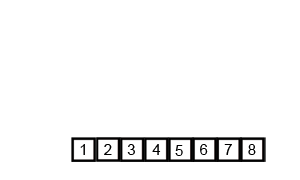
Python
#!/usr/bin/env python
class Sort:
def mergeSort(self, alist):
if len(alist) <= 1:
return alist
mid = len(alist) / 2
left = self.mergeSort(alist[:mid])
print("left = " + str(left))
right = self.mergeSort(alist[mid:])
print("right = " + str(right))
return self.mergeSortedArray(left, right)
#@param A and B: sorted integer array A and B.
#@return: A new sorted integer array
def mergeSortedArray(self, A, B):
sortedArray = []
l = 0
r = 0
while l < len(A) and r < len(B):
if A[l] < B[r]:
sortedArray.append(A[l])
l += 1
else:
sortedArray.append(B[r])
r += 1
sortedArray += A[l:]
sortedArray += B[r:]
return sortedArray
unsortedArray = [6, 5, 3, 1, 8, 7, 2, 4]
merge_sort = Sort()
print(merge_sort.mergeSort(unsortedArray))
原地归并
Java
public class MergeSort {
public static void main(String[] args) {
int unsortedArray[] = new int[]{6, 5, 3, 1, 8, 7, 2, 4};
mergeSort(unsortedArray);
System.out.println("After sort: ");
for (int item : unsortedArray) {
System.out.print(item + " ");
}
}
private static void merge(int[] array, int low, int mid, int high) {
int[] helper = new int[array.length];
// copy array to helper
for (int k = low; k <= high; k++) {
helper[k] = array[k];
}
// merge array[low...mid] and array[mid + 1...high]
int i = low, j = mid + 1;
for (int k = low; k <= high; k++) {
// k means current location
if (i > mid) {
// no item in left part
array[k] = helper[j];
j++;
} else if (j > high) {
// no item in right part
array[k] = helper[i];
i++;
} else if (helper[i] > helper[j]) {
// get smaller item in the right side
array[k] = helper[j];
j++;
} else {
// get smaller item in the left side
array[k] = helper[i];
i++;
}
}
}
public static void sort(int[] array, int low, int high) {
if (high <= low) return;
int mid = low + (high - low) / 2;
sort(array, low, mid);
sort(array, mid + 1, high);
merge(array, low, mid, high);
for (int item : array) {
System.out.print(item + " ");
}
System.out.println();
}
public static void mergeSort(int[] array) {
sort(array, 0, array.length - 1);
}
}
时间复杂度为 , 使用了等长的辅助数组,空间复杂度为 。
Reference
- Mergesort - Robert Sedgewick 的大作,非常清晰。